Geometri

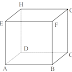
I. Kubus Kubus adalah bangun ruang yang dibatasi oleh 6 buah persegi yang kongruen Jika r = rusuk kubus maka 1.  Volume = r ´ r ´ r = r3 2.  Luas permukaan kubus tertutup = 6 ´ r2 3.  Luas permukaan kubus tanpa tutup = 5 ´ r2 4.  Panjang rusuk yang diperlukan = 12r II. Balok Balok adalah bangun ruang yang dibatasi oleh 6 daerah persegi panjang  yang terdiri atas 3 pasang yang koingruen.  p = panjang (KL = MN = OP = QR) l = lebar (KN = LM = PQ = OR) t = tinggi ( KO = LP = MQ = NR) Panjang rusuk = 4(p + l + t) Luas permukaan = 2(p´l + p´t + l´t) Volume = p ´ l ´ t III. Prisma Prisma adalah bangun ruang yang dibatasi oleh dua bidang sejajar dan beberapa bidang lain yang memotong menurut garis sejajar Luas prisma = 2´Luas alas + luas selubung prisma Volume prisama = Luas...

Konsep Barisan Deret

Standar Kompetensi Menerapkan konsep barisan dan deret dalam pemecahan masalah Kompetensi Dasar:   Mengidentifikasi pola,barisan dan  deret bilangan                                     Menerapkan konsep barisan dan deret aritmatika                                     Menerapkan konsep barisan dan deret Geometri Deret Geometri tak hingga        ...

Integral

STANDAR KOMPETENSI 1 Menggunakan konsep integral dalam pemecahan masalah Kompetensi Dasar : Memahami konsep integral tak tentu dan tertentu Rumus–Rumus Integral Tak Tentu Fungsi Aljabar 1.       ò dx  = x + c 2.       ò a dx = a ò dx = ax + c Kompetensi Dasar : Menghitung  integral tak tentu dan integral tertentu dari fungsi aljabar dan fungsi trigonometri yang sederhana Misalkan kurva y = f(x) kontinu pada interval  tertutup [a, b], maka luas daerah L yang dibatasioleh kurva y = f(x), sumbu X, garis x = a, dan garis x = b, ditentukan dengan rumus:  Integral trigonometri Integrasi fungsi trigonometri. Integral dari fungsi trigonometri terkadang melibatkan identitas fungsi trigonometri. Kompetensi Dasar : Menggunakan integral untuk menghitung luas daerah dibawah kurva dan volume benda putar Menghitung...

Logika Matematika

Standar Kompetensi Menerapkan logika matematika dalam pemecahan masalah yang berkaitan dengan pernyataan majemuk dan pernyataan berkuantor 1.      Kompetensi Dasar  1 : Mendeskripsikan ingkaran, konjungsi, disjungsi, implikasi biimplikasi dan ingkarannya Negasi (Ingkaran)             Negasi adalah pengingkaran terhadap nilai kebenaran suatu pernyataan. ~ p : tidak p Tabel kebenaran negasi Kompetensi Dasar 2.  Mendeskripsikan konvers, invers dan kontraposisi 1)      Konjungsi adalah penggabungan dua pernyataan atau lebih dengan operator “dan”. p Ù q : p dan q 2)      Disjungsi adalah penggabungan dua pernyataan atau lebih dengan operator “atau”. p Ú q : p atau q 3)      Implikasi adalah penggabungan dua pernyataan dengan operator “Jika …, maka …”. p Þ q...